We are currently at a turning point in these lessons, where the coming lessons will be exploring very different aspects of sets than those that we’ve been studying so far. Accordingly, I thought this would be a nice place to insert a lesson that may seem somewhat out of place, though is nonetheless absolutely vital to see at least once. In this lesson, we’ll see that the real numbers that we’ve seen in the previous lesson and in lesson 13 are in fact, well, real.
Before I discuss what this actually means, let me first introduce some notation that will end up being useful for us in the future. Let A and B be sets, and suppose that B is a subset of A. We’re now going to denote the phrase “B is a subset of A” as . In order to remember which set goes on which side of the “
” sign, we can think of this symbol as being similar to the “less than” symbol that we use to compare numbers. In particular, when we want to write that a number, call it “a”, is “less than or equal to a number ‘b'”, we simply write
. The similarity in appearances of this symbol with the above symbol should help the reader remember which set goes where.
There are even more similarities between the symbols and their respective meanings. Recall that since any number is less than or equal to itself (in particular, it is equal to itself), we can always write “” for any number “a”. Similarly, since any set is a subset of itself, we can always write “
” for any set A. Also recall that we can flip the direction of the “
” sign, so that “
” and “
” have exactly the same meaning. We read the former expression as “a is less than or equal to b” and we read the latter as “b is greater than or equal to a”, and clearly these reflect the same abstract idea. Similarly, we are at freedom to write “
” or to write “
” to express the same meaning. We read the former as “A is a subset of B” and the latter as “B contains A”.
Lastly, we recall that when we compare numbers we have the extra symbol “”. If we write “
”, then we’re saying that “a” is strictly less than “b”, meaning that “a” is actually less than “b” and not equal to it. Similarly, we employ the symbol “
” to denote the same idea when comparing sets. Thus, when we write “
”, we mean that A is a subset of B and is not equal to B, so that every element in A is in B but that there is at least one element in B that is not in A. Note that if
, then
, but it is not the case that if
then
, simply because in the latter case “
” provides a counterexample. Thus, we’re always safe in writing “
”, because the meaning of that expression contains the meaning of the expression “
”. The latter expression, however, carries more information in it (namely that
), so we have to be a bit more careful when we use it.
Now why am I introducing this notation here? I do so because it will help us compare some of the important sets we’ve seen so far. Recall that we’ve considered the set of natural numbers, which we (and everyone) denote by , and which consists of the elements
. We also have the set of integers, which we denote by
, and which consists of the positive and negative whole numbers:
. Next, we have the set of fractions, both positive and negative, which we denote by
. This set consists of the expressions
where
, and where we consider two of these expressions the same if one can be “reduced” to the other. Thus,
. We often call an element of
a rational number (for more on this set, see lesson 11). Lastly, we have the real numbers, which is in some sense the set of all numbers. For now, we can think of this set as the set of all expressions of the form
where and each
. With all of the above notation, we have that
.
If you’ve read lesson 13 then you’ll know that I could also have written since
has a larger infinite cardinality than
does, but since that was an “optional” lesson I decided to use the
symbol (because it’s not necessarily clear that these sets are not equal unless you’ve read that lesson). I’m warranted in using this because it is known that any fraction can be expressed as an infinite decimal, and is therefor an element of
. What is not obvious, however, is that
. I.e., it is not obvious that there are numbers that can be written as infinite decimals but cannot be written as a fraction. The rest of this lesson will show this fact.
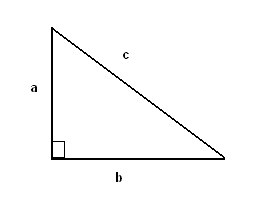
In particular, we’ll show that the square root of two (i.e., that number which, when multiplied to itself, gives you 2), written as , cannot be written as a fraction. Why is this significant? Well,
is in a very clear sense a “real” number, in that it plays a key role in very practical mathematics. For example, if we consider a right triangle like that shown in figure 1, and if we let the side lengths of “a” and “b” both equal 1, then Pythagoras and his theorem tell us that the length of “c” is
(via the famous and likely familiar formula
). We obviously want to have a system of numbers that describes this basic geometric object, and therefore
has a very real and necessary existence.
We’ll now show that cannot be written as a fraction, and is therefore irrational. We use this terminology because numbers that are not fractions are then, by definition, not rational numbers (defined above), and in a very clear way the numbers that aren’t fractions are seemingly “less real” and/or “less tangible” simply because they have this elusive quality of having an infinitely long and chaotic expression as a decimal. The fact that
is irrational (which we’ll now show) gives credence to the idea that these numbers, despite their strange and unintuitive expressions, are very “real”.
Now, how do we prove that is not a fraction? Well, as in most proofs of “negative” statements (A is not this, B does not do this, etc.), our most powerful weapon is that of proof by contradiction. Thus, we suppose that
, and we further suppose that
is already “fully reduced”, meaning that there are no common factors between “a” and “b”.
Now, the facts that we need in order to find a contradiction (and therefore take this proof down), are the following.
Fact 1) An odd number times an odd number is again an odd number. I won’t prove this rigorously, but you can see it be realizing that “an odd number times an odd number” is really just “an odd number added to itself an odd number of times”. If I add an odd number to itself an even number of times, I get an even number , but if I do so an odd number of times I get an odd number (
).
Fact 2) An even number “a” can always be written as “2 times some other number”, where this “other number” can be either even or odd. This is, in fact, just the definition of something being even. Thus, if “a” is even, then for some
.
Fact 3) If is “fully reduced” as we’ve described above (and which can always be done), then it can’t be the case that they’re both even, for otherwise we could reduce it further by dividing out a 2 (since they’re both 2 times some other number).
Fact 4) Any whole number is either even or odd—never both and never neither.
Now, we’ve supposed that with
being fully reduced. By squaring both sides, we then find that
, and by multiplying both sides by
, we get that
. Thus,
is even, because it’s “2 times some whole number”. But if
is even, then so is
, because if
were odd then
would be odd by Fact 1), and so
must be even by Fact 4). By Fact 2), we have that
for some k. Thus, we have that
. Multiplying both sides by
(and not writing the “
” symbol), we have that
, which, after dividing both sides by 2, gives
. But this means that
is even, and thus that
is even (by the same logic as above). Thus both “a” and “b” are even, which contradicts Fact 3) since we assumed that
was fully reduced.
Thus we’ve found our contradiction, which means our supposition was wrong, which means that cannot be written as any fraction, which means that irrational numbers are something we have to confront if we wish to even ask about the third side of the triangle in figure 1. In fact, it turns out that there are way more irrational numbers than there are rational ones, which is what makes it possible for
to be so much more massively infinite than
, as we saw in lesson 13. Of course, it’s not the case that all irrational numbers are as fundamental and necessary as
, but lots of them are (another famous one is
), and so we must view them as “existing” in the same way that the more intuitive notions of fractions and whole numbers do. Negative numbers might be another cause for concern as to how “real” they are, but we’ll see in the next few lessons that these are also quite necessary, and therefore “real”.
This proof is a little “out of place” in the sense that we could have very easily plowed forward with our math without ever going over it. However, just as no one should live and die without ever hearing Beethoven’s Symphony No. 5 or watching The Godfather, no one should live and die without seeing this proof. This, along with Euclid’s proof that there are infinitely many prime numbers, are two examples of math that should be “common knowledge”. They show the type of ingenuity that goes into mathematical reasoning, and they establish deep facts about one of the most eternal and objective structures that logic has access to: that of the number.
In the coming lessons we adopt a radically new and extremely powerful perspective on objects and processes that may have previously seemed trivial, simple, and/or meaningless. We not only reconsider high school mathematics, as we did in the previous lesson, but we also reconsider middle and elementary school mathematics. Indeed, we simply “rebuild” a lot of this math using our new set-theoretic formalism, but with a whole new twist.
I also want to have a quick recap of all of the notation that we’ve developed so far, so that it can easily be referenced from the same place. If you already feel comfortable with all of that, then go right on to the next lesson. The recap is more for referring back to as we continue to build up more complicated (but not at all scary) notation.
With all due respect, I think if you used the notation for ‘is a subset of ‘ to describe rational numbers and real numbers, you should use the same notation to relate natural numbers and integers, rather than using the ‘is a proper subset of ‘ notation.
I do see what you’re getting at, but I’m just using that as an opportunity to show the difference between the two relationships. In the sentence immediately following that chain of inclusions, I discuss why it is that we can actually use “is a proper subset of” in the last line, but that we don’t yet know for sure that’s the case. I’m using that to bring out how we need to be more careful with one of the symbols than we do the other. I end up adopting the more standard notation of always using “is a subset of” (as opposed to “is a proper subset of”) in later lessons, but I figure this is a good place to point out why one is “better”. Thanks for pointing that out, though, and hopefully if anyone is confused by it they’ll come check out the comments for a bit more discussion.
Hello!
I have discovered your lessons last week and i can’t prevent myself from coming here to learn something new everyday!
So for that i want to say Thank You So much! For some reason, i had to stop studying maths after high school, and study medicine but thanks to you and your excellent lessons, i can still learn some beautiful mathematical stuff!!!
So the natural question that comes to my mind is: did you stop
stop writing new lessons?
If the answer is yes, i really beg you to reconsider that! Because Your lessons are wonderful and accessible!!
My second question has more to do with the topic: here you argue that N is included in Z but in a previous lesson, you showed that they do have the same cardinal! I understand that N can’t be equal to Z because for instance -1 is not in N but i am a little bit confused here!
Thank You for everything (again)
Hi there! I am indeed still writing lessons, albeit with a much lower frequency than I would like to these days for reasons that will be clearer in a couple of months hopefully. That said, I do hope to get some new lessons up in the near(ish) future, and I’m glad you’re enjoying the lessons!
As for your question about Z and N, you’re entirely warranted in being confused. Namely, it is indeed the case that N and Z are different sets, AND it is also the case that they have the same cardinality. Recall that one of the strange things about infinite sets is that they can “seem” bigger or smaller than other infinite sets while still having the same cardinality — the important thing is whether or not there is a bijective function between the two sets in question, and this may be the case even if there “seems” to be more elements in one set!
Let me know if you would like some more explanation, and I hope you keep enjoying the site!
Cheers